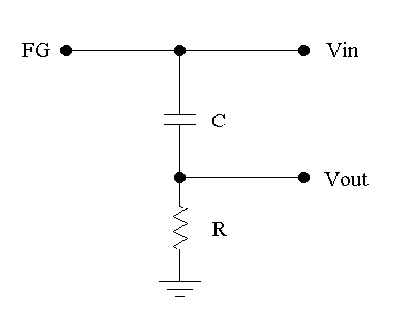
High-pass filter frequency response

Having available the gain and phase shift equations for the high-pass filter:

• Interchange R and C and repeat the steps outlined for the low-pass filter to graph log G(f) vs. log(f) and φ(f) vs. log(f) for a high-pass filter.
  Use either the Vout,Δt or the Lissajous method to determine G and φ for your well-chosen set of frequencies that should include f₀.

Note the similarities between the low-pass and high-pass filters.

• Compare the centre frequencies f₀.
• Compare the filter gains and phase shifts at f₀.
• How do the phase shifts of the two filters differ? Do the output signals lead or lag the input signals?
• Compare the roll-off rates. What is the order of these filters?

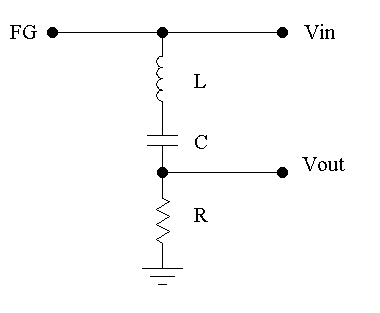
RCL band-pass filter

Adding an inductor L to an RC circuit produces a band-pass filter that passes frequencies within a certain range while attenuating frequencies outside that range.

• Setup your circuit as shown with an inductor L = 2.2mH, C = 0.01μF and R = 100Ω.
• Set the FG to 5V_pp sine wave.
• Sweep the frequency and note qualitatively the changes in gain and phase shift between the input and output signals. You do not need to tabulate G(f), φ(f).
• Note the frequency f_bp where the G=V_out/V_in is a maximum.
• What is the phase shift φ between V_in and V_out at f_bp?

The RCL circuit is also capable of resonant oscillations (ringing). The energy-dissipating element R causes the oscillation of frequency f₀ = 1/(2π√(LC)) Hz to decay exponentially with a time constant τ = L/R.

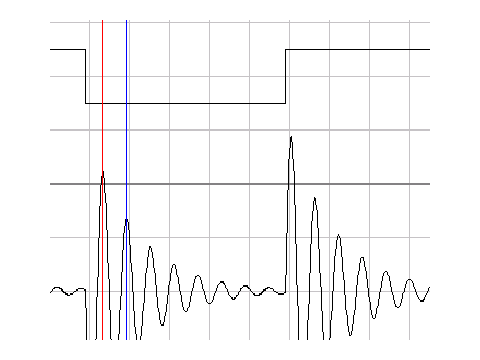
Driving the RCL circuit with a rapidly changing voltage such as a square wave will cause the circuit to undergo such damped oscillations, as shown. To view this effect:

• determine f₀ for this filter, using measured RCL values;
• set the FG to output a 5V_pp square wave of about 0.1 f₀;
• zoom into the waveform and measure the gain and time of two points on adjacent peaks of the ringing signal.
• Determine the ringing frequency f₀;

For an exponential ringing decay envelope V = V₀ exp(-t/τ),
the decay time constant is given by τ = (t₁ - t₂)/(ln V₂ - ln V₁)

• Use this equation to estimate τ
• Compare your results for f₀ and τ with those predicted by the theory. Do the results agree within experimental error?
• Compare your f₀ results with the previously estimated f_bp.